You can put this solution on YOUR website!Factor out eˣ d/dx (eˣ) = lim h→0 (1/h) eˣ eʰ 1 Since e^x does not contain h, it can be factored out of the limit completely d/dx (eˣ) = (eˣ) lim h→0 (1/h) eʰ 1 But remember we previously established that eʰ = lim h→0 (1h) So, let us substitute this into the derivative1 Answer1 Active Oldest Votes 3 Always check the complementary solution, y ″ − y = 0, before identifying a particular solution y ″ − y = 0 has a solution of the form y = C 1 e x C 2 e − x Since the right handside, e x, is a term in the complementary solution you can usually try multiplying the particular solution that you would
Ocw Mit Edu Resources Res 6 012 Introduction To Probability Spring 18 Part I The Fundamentals Mitres 6 012s18 L07 Pdf
Y e x
Y e x-答案解析 为求原方程的通解,可用参数变易法:把积分常量C₁改为x的某个函数u,得:y=ue^ (x) (1) 将 (1)的两边对x取导数得dy/dx=e^ (x) (du/dx)ue^ (x) (2) y= (xC)e^ (x) 齐次方程 解析看不懂? 求助智能家教解答The exponential function is one of the most important functions in calculus In this page we'll deduce the expression for the derivative of e x and apply it to calculate the derivative of other exponential functions Our first contact with number e and the exponential function was on the page about continuous compound interest and number eIn that page, we gave an intuitive




Working With Exponentials And Logarithms
X^y =e^xy The basic trick here is to remove the variable from the exponent In this case,we can take help of "ln" opereation or,lnx^y=lne^xy Taking ln on both sides or,ylnx=xylne logx^n=nlogx(1) Now,this equation can easily be differentiated or,yd/dx(lnx)lnxd/dx(y) =d/dx(xy) Here lne=1 and d/dx(uv)=ud/dx(v)vd/dx(u)Mine has on it I can just keep punching in and then punch You'll have and If you don't have it, ,Take the logarithm of both sides So you get logx = y(log(e)) Some rearranging gives
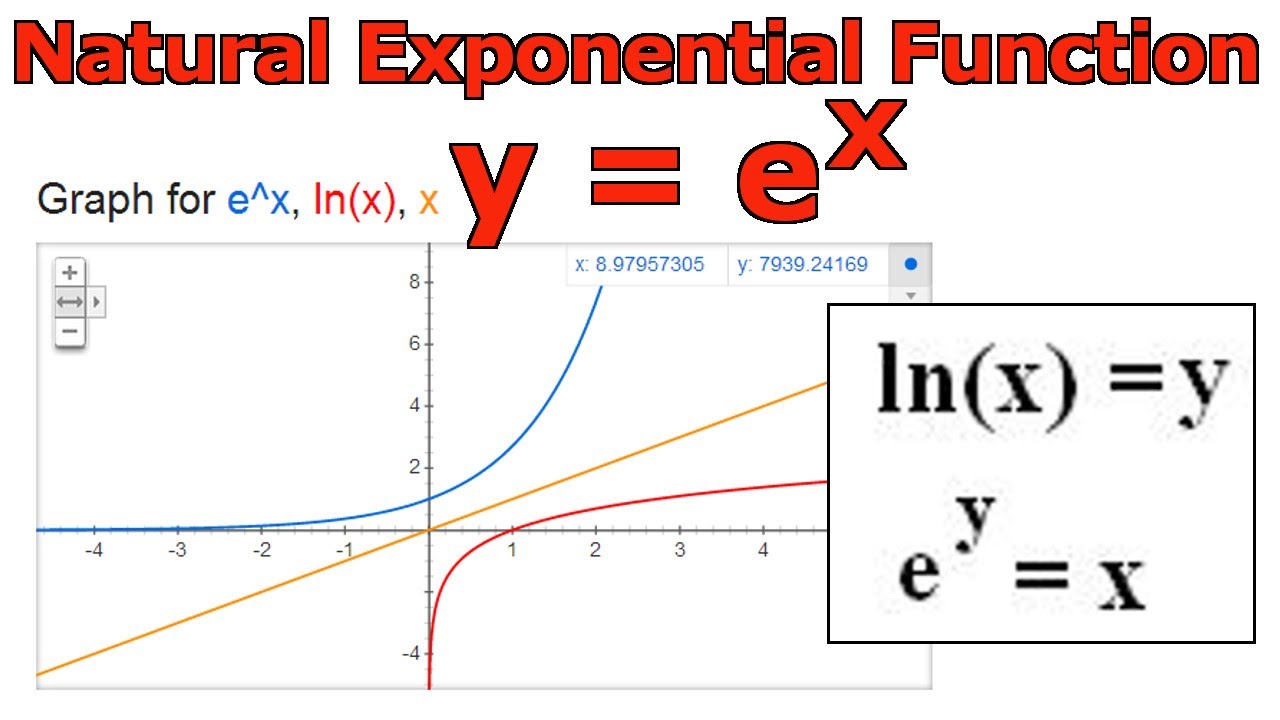
Do you have a calculator?Definition 2 The exp function E(x) = ex is the inverse of the log function L(x) = lnx L E(x) = lnex = x, ∀x Properties • lnx is the inverse of ex ∀x > 0, E L = elnx = x • ∀x > 0, y = lnx ⇔ ey = x • graph(ex) is the reflection of graph(lnx) by line y = x • range(E) = domain(L) = (0,∞), domain(E) = range(L) = (−∞,∞)EX Y = ypY (y)= EX y • In stick example EX=EEX Y = EY/2 =!/4 var(X Y) and its expectation Section means and variances
Graph y=e^x1 y = ex − 1 y = e x 1 Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = −1 y = 1 Horizontal Asymptote y = −1 y = 1 How do you find the derivative of #Y= (e^xe^x)/(e^xe^x)#?9 Let the random variable X have the N ( 0, 1) distribution for which the probability function is f ( x) = 1 2 π exp ( − x 2 2), − ∞ < x < ∞ Let Y = e X A Find the probability density function for Y, B Find E ( Y), C Find E ( Y 2) and deduce V a r ( Y)




Expected Value Of A Binomial Variable Video Khan Academy



Function And Relation Library
If yx = ey x prove that dy/dx = (1 log y)2/log y Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to getClick here👆to get an answer to your question ️ Area bounded by the curves y = e^x, y = e^x and the straight line x = 1 is (in sq units)Answer to Solve the initial value problem x y' y = e^x, y(1) = 2, t greater than 0 By signing up, you'll get thousands of stepbystep
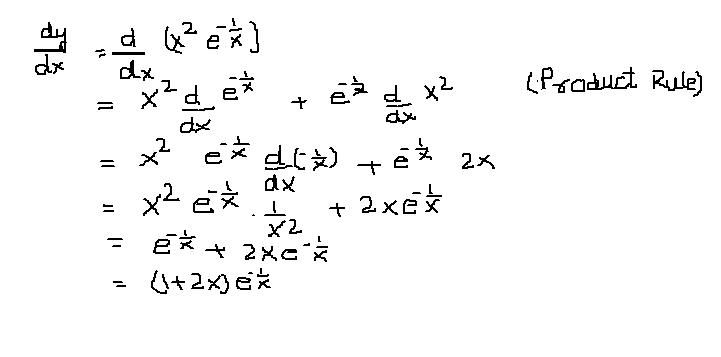



How Do You Find The Derivative Of Y X 2 E 1 X Socratic
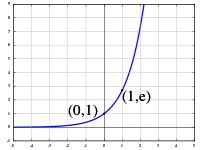



Exponential Function Wikipedia
y=e^xやの微分を行ってみようy=e^axの微分はどうなるのか それでは、まず数式y=e^xの微分を行ってみましょう。 y=e^xの微分は定義そのものといえますが、元の数式と同じy=e^xのままとなります。これは定義ですので覚えるしかないです。 ※Lecture 26 Conditional expectation Scott She eld MIT Lecture 26Click here👆to get an answer to your question ️ If x^2e^y 2xye^x 13 = 0 , then dydx is
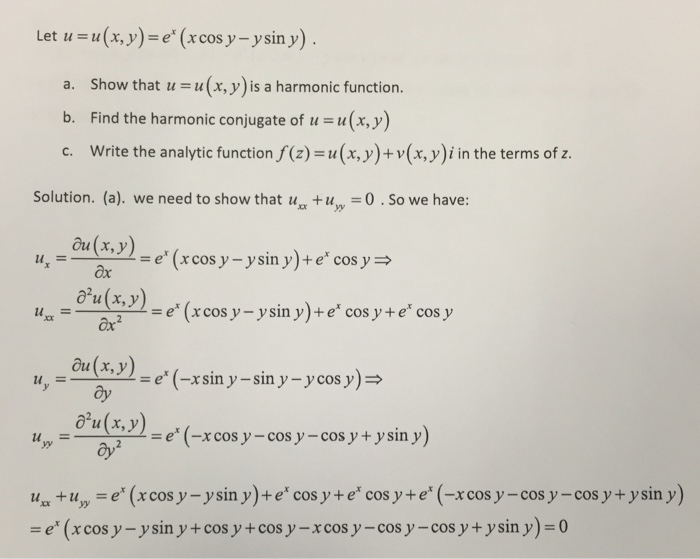



Let U U X Y E X X Cos Y Y Sin Y Show That Chegg Com




The Logarithm And Exponential Functions
If X and Y are random variables such that E2X Y = 0 and EX 2Y = 33, then EX EY = _____Видеоурок Число e Функция y=e^x, ее свойства, график, дифференцирование по предмету Алгебра富山大学経済学部 経営経済の基礎数学ii 第7 回演習プリント() 学科( で囲む)済・営・法・その他 学籍番号 氏名



Logarithms




The Solution Of The Differential Equation Dy Dx 1 E X Y I
Y=e^x Loading y=e^x y=e^x Log InorSign Up y = e x 1 y = kHistory The idea of the expected value originated in the middle of the 17th century from the study of the socalled problem of points, which seeks to divide the stakes in a fair way between two players, who have to end their game before it is properly finished This problem had been debated for centuries, and many conflicting proposals and solutions had been suggested over the years,In der Mathematik bezeichnet man als Exponentialfunktion eine Funktion der Form ↦ mit einer reellen Zahl > als Basis (Grundzahl) In der gebräuchlichsten Form sind dabei für den Exponenten die reellen Zahlen zugelassen Im Gegensatz zu den Potenzfunktionen, bei denen die Basis die unabhängige Größe (Variable) und der Exponent fest vorgegeben ist, ist bei




Variation Of Parameters Y 2y Y E X 1 X 2 Youtube




Introduction We Are Going To Look At Exponential Functions We Will Learn About A New Special Number In Mathematics We Will See How This Number Can Be Ppt Download
x y = e (xy) Taking log of both sides \(\Rightarrow\) log x y = log e (xy) \(\Rightarrow\) ylog x = (xy) log e \(\because\) log e = 1 \(\Rightarrow\) ylog x = (xy) \(\Rightarrow\) y log xy = x \(\Rightarrow\) y = \(\frac{X}{1logX}\) \(\Rightarrow\) \(\frac{dy}{dX}\) = \(\frac{(1logX)1X\big(0\frac{1}{X}\big)}{(1logX)^2}\)Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history Daniel的学习笔记 浙江大学计算机专业15级硕士在读, 方向 Machine Learning, Deep Learning, Computer Vision blog内容是我个人的学习笔记, 由于个人水平限制, 肯定有不少错误或遗漏




If A X Y Y E X X In R A N D B X Y Y E X X




Probability Covariance And Correlation Faisalkhan81 Yahoo Com
I have an equation I need to solve by using undetermined coefficients y'' y' = e x The auxiliary equation is r 2 r = 0 , so 2 real roots (R 1 =0, R 2 = 1) So, y c (x) = C 1 C 2 e x Now for the particular solution I can try Ae x but this is already present in the complementary solution Do Answer x x y x y =e x y =e x−y x y =e x−y , then x y =e x−y , then dx x y =e x−y , then dxdy x y =e x−y , then dxdy x y =e x−y , then dxdy is equalLimit Definition Proof of e x Limit Definition By laws of exponents, we can split the addition of exponents into multiplication of the same base Factor out an e x We can put the e x in front of the limit We see that as h approaches 0, the limit will get closer to 0/0 which is an indeterminant form (meaning we don't really know what is




Show That Var X E X 2 If E X 0 Show That Chegg Com



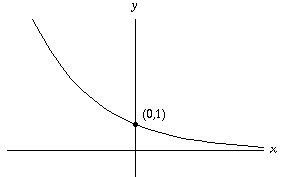
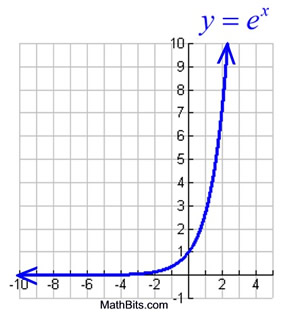
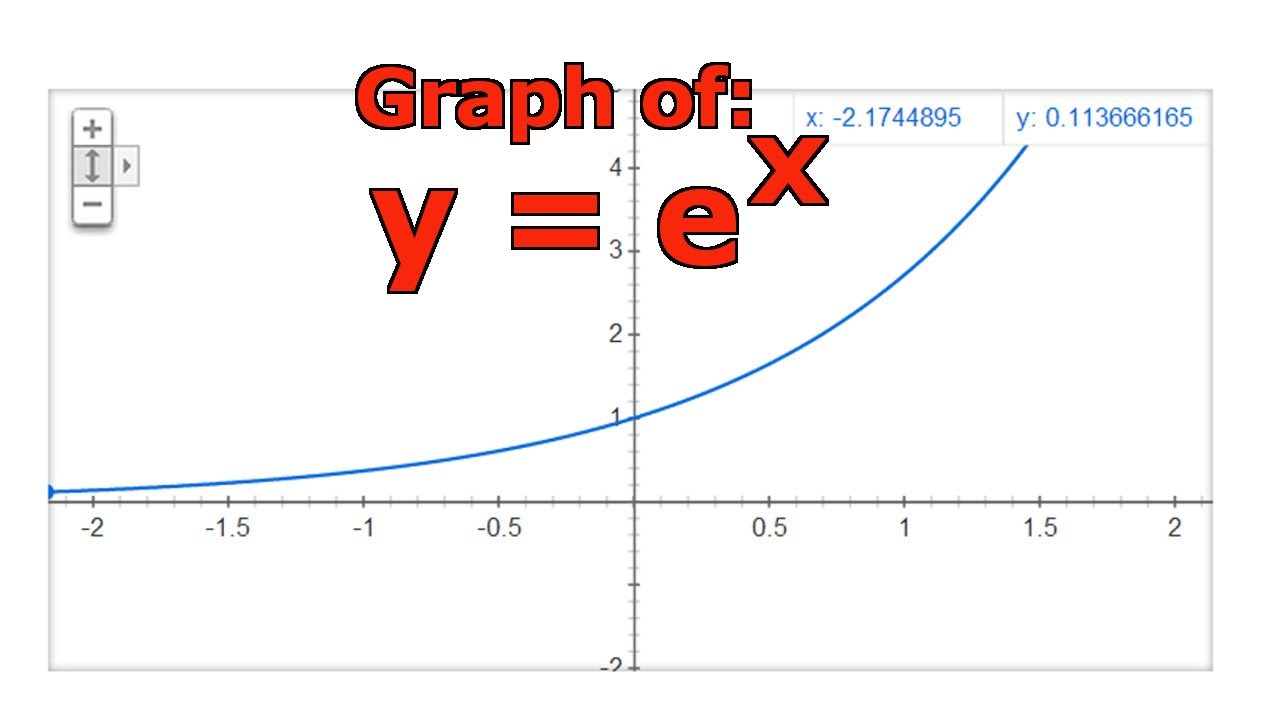
What Is The Domain And Range Of Y E X Socratic
– Law of iterated expectations y • EX Y = y= (number) 2 – Law of total variance • Sum of a random number Y of independent rv's EX Y= (rv) 2 – mean, variance • Law of iterated expectations EEX Y =!Graph y = e x;Algebra Graph y=e^ (x) y = e−x y = e x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0




If Y E X E X E X E X Prove That Dy Dx 1 Y 2




General Solution Of Differential Equation Y 3y E X Mathematics Stack Exchange
Using the formulas of integration ∫ e x d x = e x , we get e y = e x c ⇒ y = ln ( e x c) This is the required solution of the given differential equation ⇐ Solve the Differential Equation dy/dx=xy^2 ⇒ Solve Differential Equation dy/dx=xe^y ⇒LYE x Crissa "Ace" Jackson ️💪🏽🏀 Follow us on tik tok @LYE_Academy 8686 2 Comments 9 SharesCalculus Basic Differentiation Rules Quotient Rule 1 Answer Ratnaker Mehta #(dY)/dx=4/(e^xe^x)^2# Explanation To find the derivative, we have to use the Quotient Rule, and, the Chain Rule, given below for ready reference The Quotient



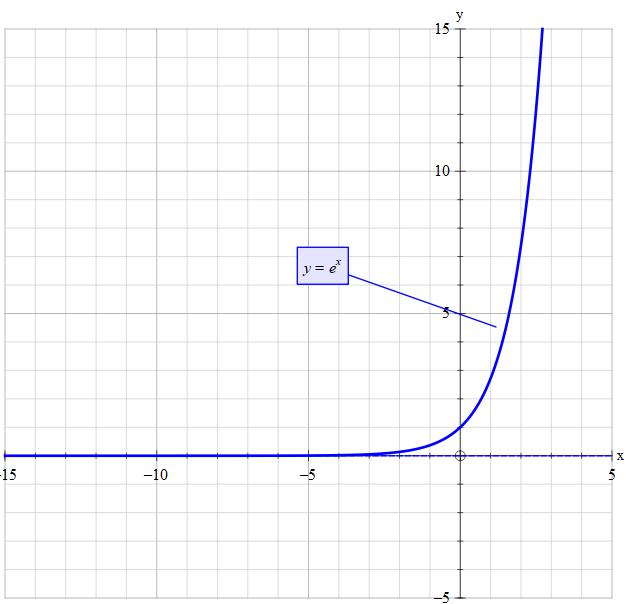
Solution Y E X How Do I Graph This Please Help




Working With Exponentials And Logarithms
E (Y) = Sum (y P (Y = y)) where P (Y = y) is the probability that the random variable Y takes on the value y, and the sum extends over all possible y In a similar fashion E (X Y) = Sum (z P (X Y = z)) where the sum extends over all possible values of zSo, an inverse to a function is found by switching the y and x terms in an equation Your function would be y=e^x Switching the x and y gives you x=e^y That doesn't say anything particularly intuitive So how do you bring the y term down from the exponent?The slope is \displaystyle {1} Explanation As we are seeking a tangent at \displaystyle {\left ( {5}, {1}\right)} , the curve \displaystyle\frac { {e}^ { {x}}} { {\left ( {x} {y}\right)}^ { {3}}}= {C} The slope is 1 Explanation As we are seeking a tangent at (5,1) , the curve (x y)3ex
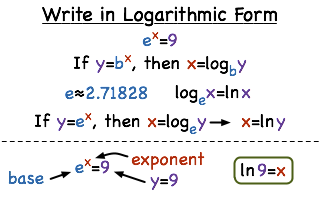



How Do You Convert From Exponential Form To Natural Logarithmic Form Printable Summary Virtual Nerd
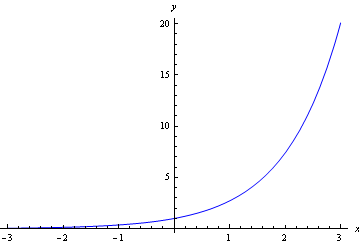



Exponential Functions
Answer to Solve the differential equation x dy/dx y =e^x, x>0 By signing up, you'll get thousands of stepbystep solutions to your homework Explanation Differentiating ex ey = exy ex ey dy dx = exy(1 dy dx) or ex ey dy dx = exy exy dy dx or ey dy dx − exy dy dx = exy −ex or (ey −exy) dy dx = (exy 3 Eliminate the exponent Using the rules of logarithms, this equation can be simplified to eliminate the exponent The exponent within the logarithm function can be removed as a multiple in front of the logarithm, as follows ln y = x ln a {\displaystyle \ln y=x\ln a} 4 Differentiate both sides and simplify



1 E X Graph
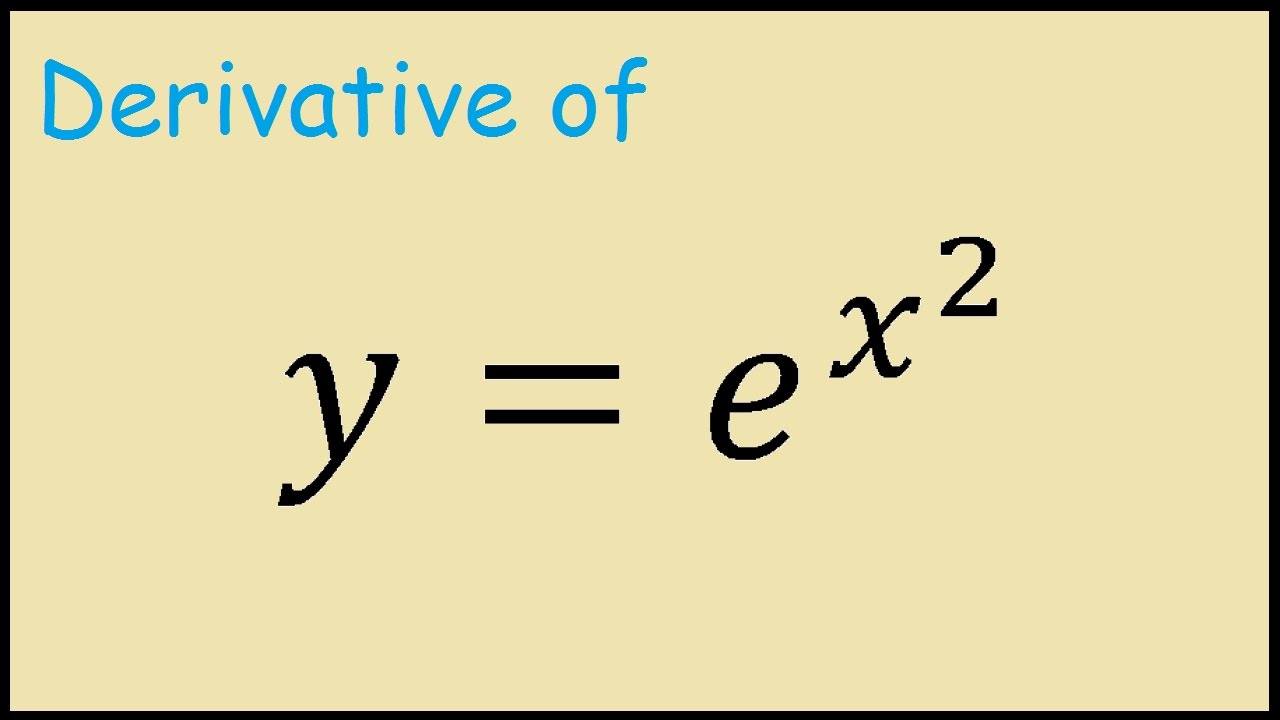



Derivative Of Y E X 2 Youtube
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyThis might feel a bit more difficult to graph, because just about all of my yvalues will be decimal approximations But if I round off to a reasonable number of decimal places (one or two is generally fine for the purposes of graphing), then this graph will be fairly easy Ex 93, 5 Form a differential equation representing the given family of curves by eliminating arbitrary constants 𝑎 and 𝑏 𝑦=𝑒^𝑥 (𝑎 cos〖𝑥𝑏 sin𝑥 〗 ) Since it has two variables, we will differentiate twice 𝑦=𝑒^𝑥 (𝑎 cos〖𝑥𝑏 sin𝑥 〗 ) Differentiating Both Sides wrt 𝑥 𝑑𝑦/𝑑𝑥=𝑑/𝑑𝑥 𝑒^𝑥



1



Www Stat Auckland Ac Nz Fewster 325 Notes Ch3annotated Pdf
How to plot a y=e^x function Follow 221 views (last 30 days) Show older comments Monica DelaCruz on Vote 0 ⋮ Vote 0 Edited Stephen Cobeldick on I have the task to plot a graph using the function y=e^x but I am having trouble with the constant eSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Bestmaths




Ex 9 1 8 Determine Order Degree Y Y E X Class 12



Definition Of Covariance The Covariance Of X Y




Show That Y E Msin 1x Is A Solution Of The Differential Equation 1 X 2 Y2 Xy1 M 2y 0
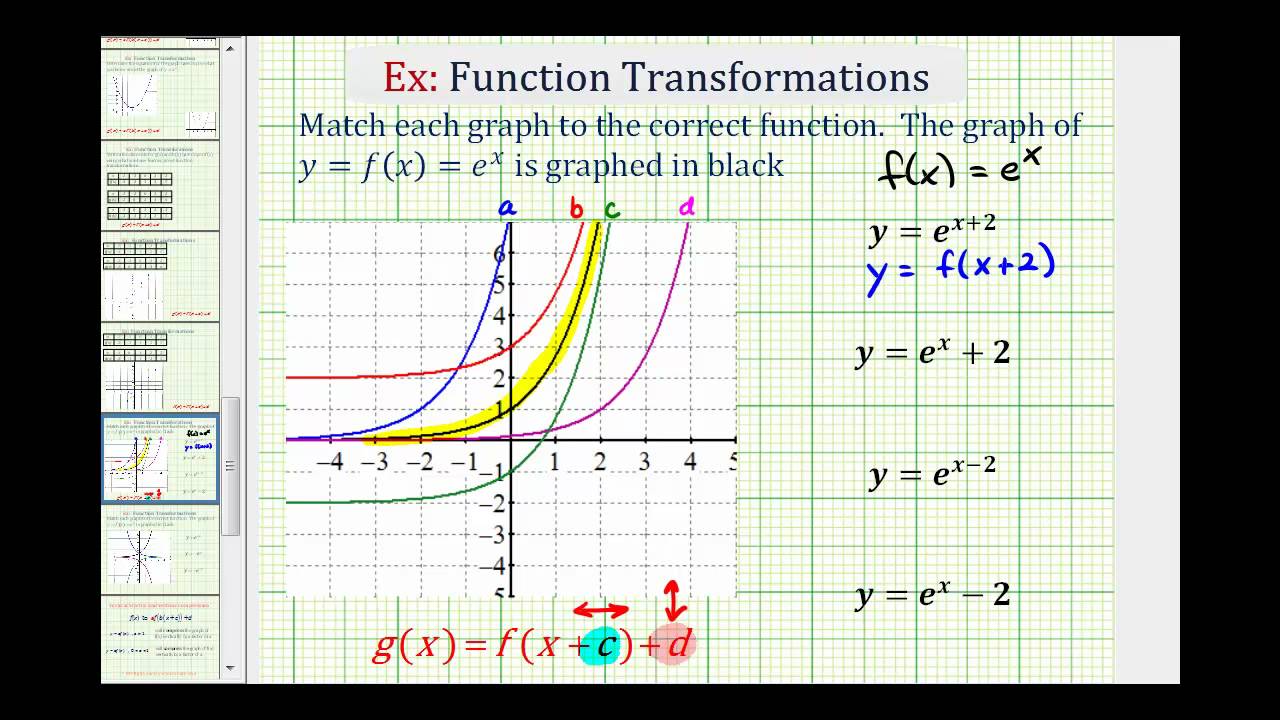



Horizontal And Vertical Translations Of Exponential Functions College Algebra




X E Y Zonealarm Results
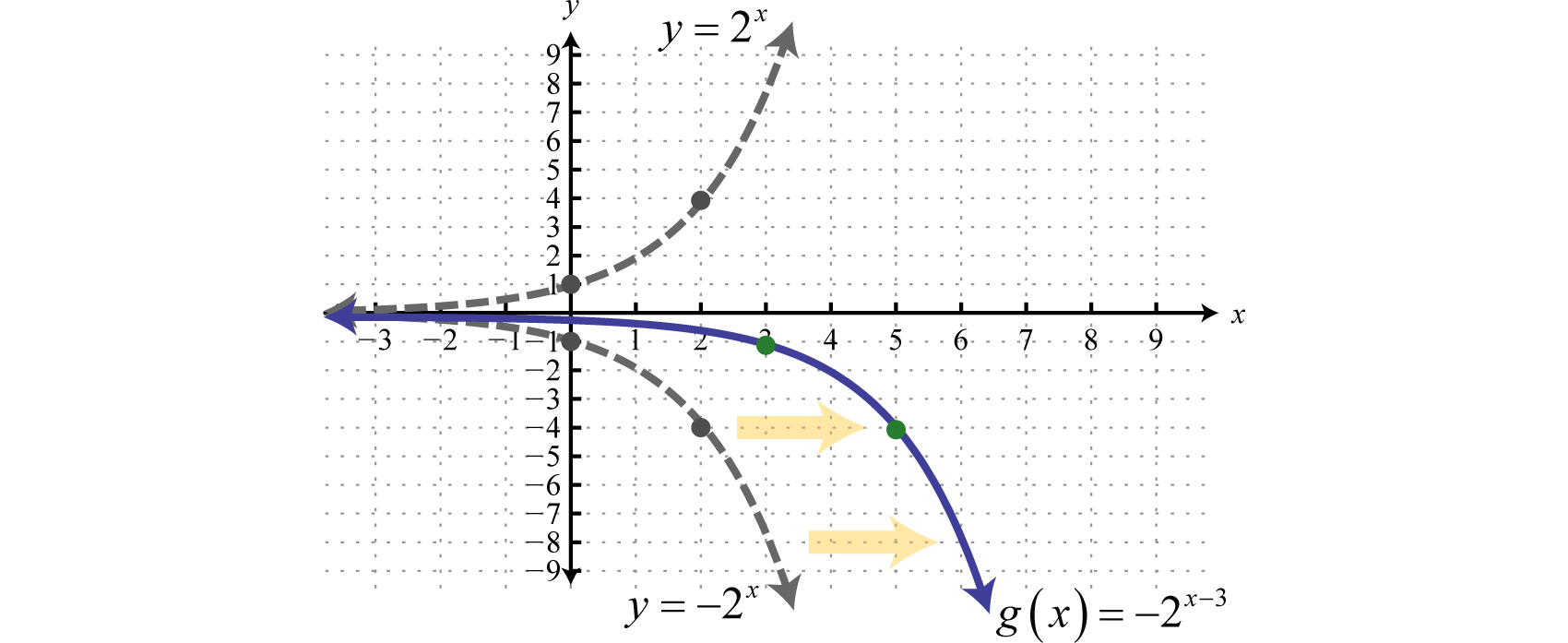



Exponential Functions And Their Graphs




Ex 9 5 10 Show Homogeneous 1 Ex Y Dx E X Y 1 X Y



Q Tbn And9gcsqdohwlqv7hezevkttjajjqlrfahan470gq5zvj62tldxf6ujk Usqp Cau




12 3 Exponential Functions




Solve X Dy Dx Y X 1 Ex Brainly In



If X Y E X Y Show That Dy Dx Logx Log Xe 2 Sarthaks Econnect Largest Online Education Community



Exponential Functions And Their Graphs




Solve D 2 3d 2 Y E E X Using Method Of Variation Of Parameters Mathematics Stack Exchange



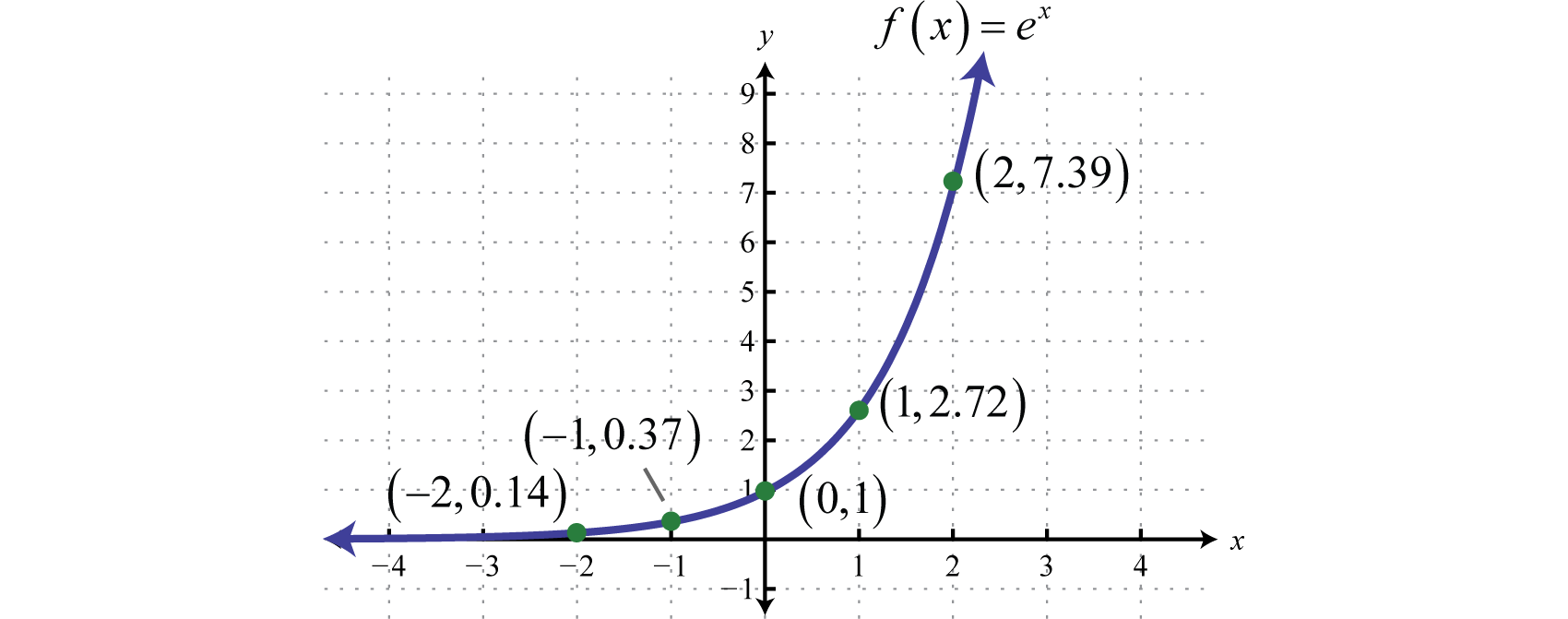
Euler S Number E
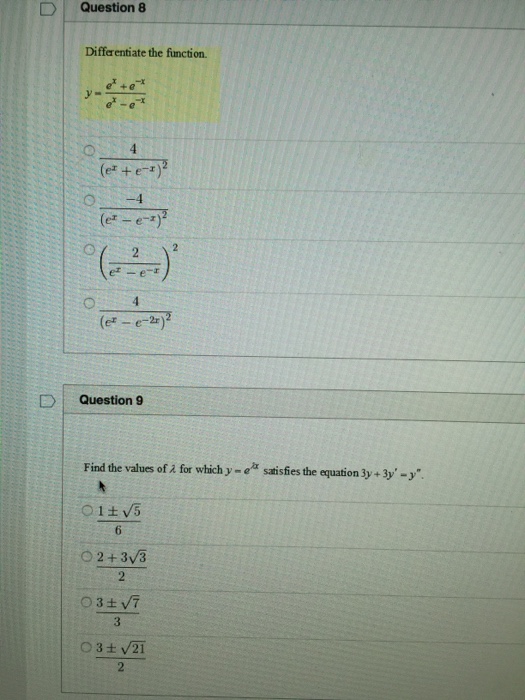



Differentiate The Function Y E X E X E X E X Chegg Com




Transforation Of Exponential Graphs Y Ex Matching Cards With Answers Teaching Resources




Differentiation Of The Exponential Function E X And Natural Logarithms Lnx Exponential Function E X Ppt Download
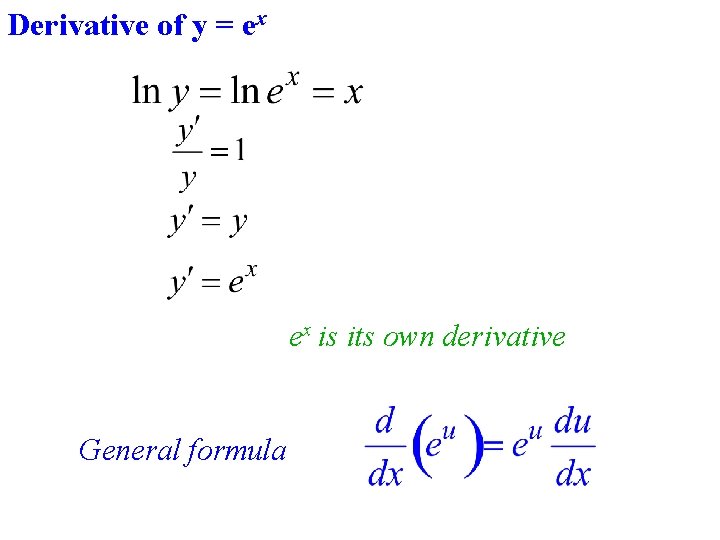



7 1 Introductionfunctions And Inverses A Function Is



Content Graphing Logarithmic Functions



1



Natural Exponential Function Y E X Youtube




Graph The Function Not By Plotting Points But By Chegg Com
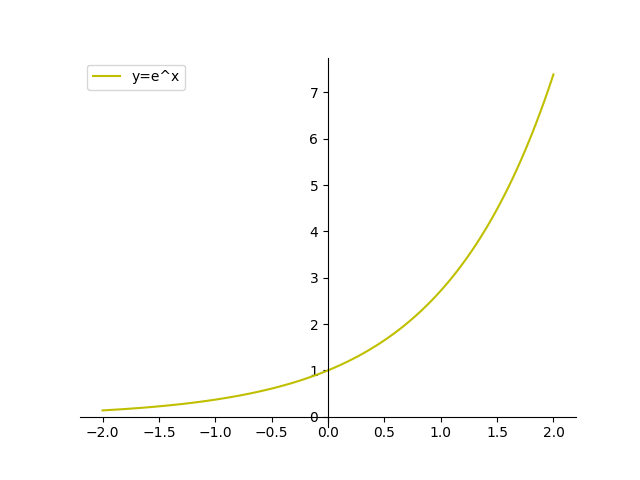



Plot A Function Y F X In Python W Matplotlib




Exponential Function Wikipedia




Review



Y E X Zonealarm Results



What Is The Graph Of E X Quora



How To Sketch The Graph F X E X 1 Socratic



Derivative Of E X Wyzant Lessons



Area Of A Surface Of Revolution




If Y Ex Tan 1 X Prove That 1 X2 D2y Dx2 2 1 X X2 Dy Dx 1 X 2 Y 0 Maths Continuity And Differentiability Meritnation Com
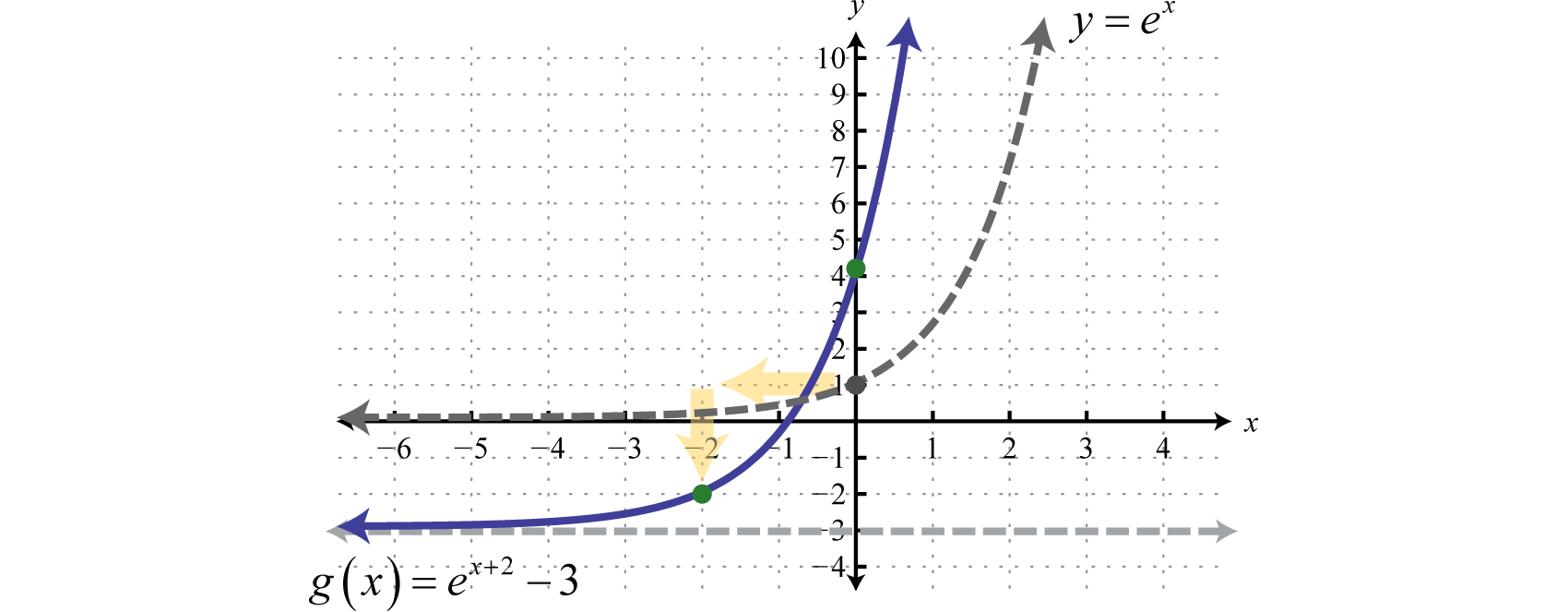



Exponential Functions And Their Graphs




The Solution Of The Differential Equation E X X 1 Dx Ye Y X




E Mathematical Constant Wikipedia



Um Math Prep S14 1 Graphs To Memorize




How To Draw Graph Of F X E X2 Quora



Solve The Equation D 2 2d 1 Y E X 3 Sarthaks Econnect Largest Online Education Community



6 Derivative Of The Exponential Function




15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts



Natural Exponential Function And Natural Logarithmic Function Mathbitsnotebook Ccss Math



Graphing The Natural Exponential Function Y E X Youtube




Working With Exponentials And Logarithms



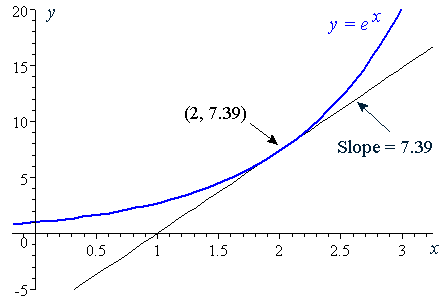
Solution Use The Graph Of Y E X To Evaluate E 1 6 To Four Decimal Places



Ocw Mit Edu Resources Res 6 012 Introduction To Probability Spring 18 Part I The Fundamentals Mitres 6 012s18 L13as Pdf
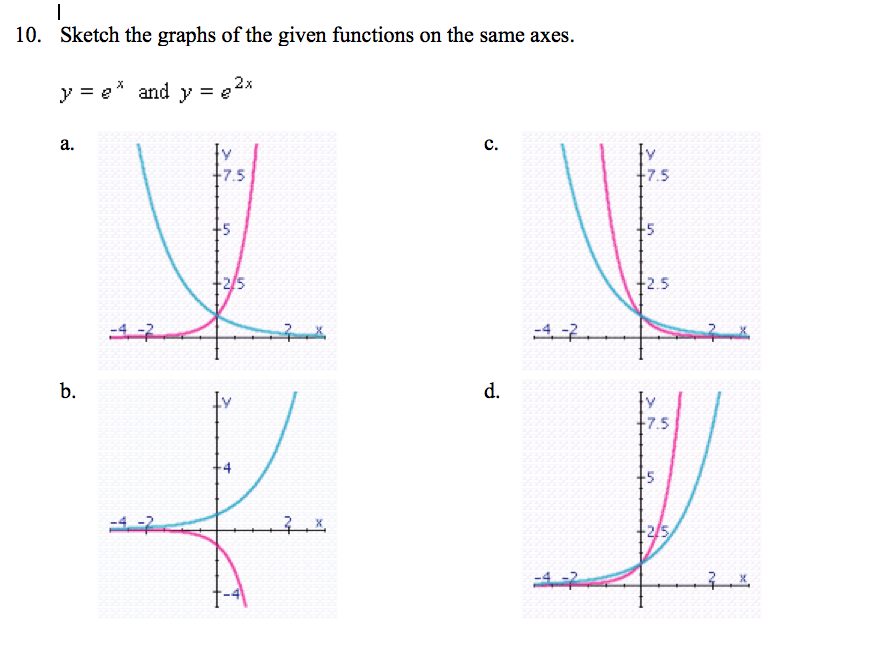



Sketch The Graphs Of The Given Functions On The Same Chegg Com



If Ex Ey Ex Y Then Dy Dx Quora



Euler S Number E




Review




Solve D 3y Dx 3 3 D 2y Dx 2 3 Dy Dx Y E X 2 Mathematics 2 Question Answer Collection



Solution Can We Sketch And Describe These Composite Functions Combining Functions Underground Mathematics




If Y Ex Sin X Prove That D2y Dx2 2 Dy Dx 2y 0 Explain In Great Detail Mathematics Topperlearning Com 5p09j033




Calculus Section 5 3 Differentiate Exponential Functions If F X E X Then F X E X F X X 3 E X Y E X X Examples Find The Derivative Y Ppt Download
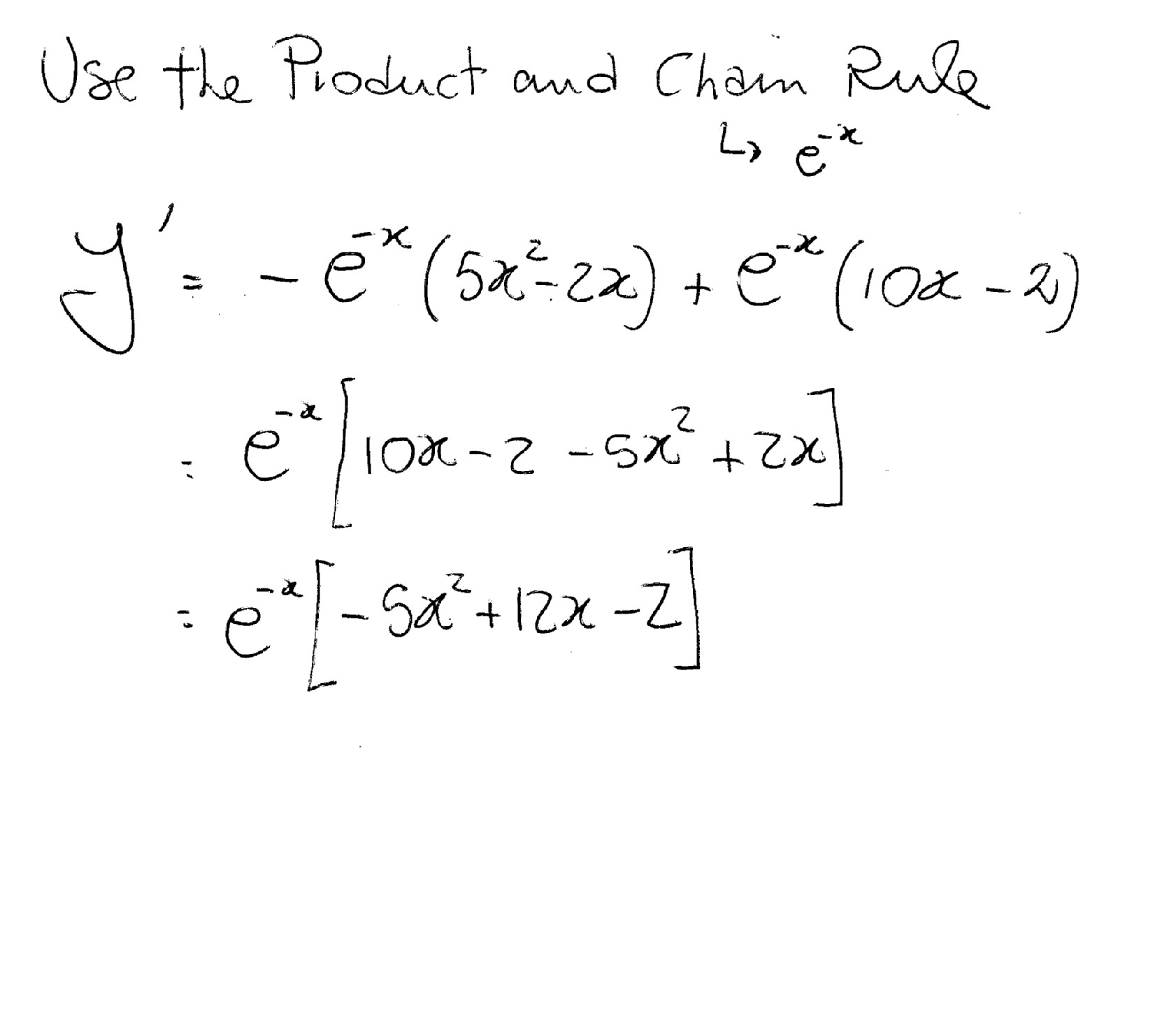



How Do You Find The Derivative Of Y E X 5x 2 2x Socratic




Resuelva Por Coeficientes Indeterminados Y Variacion De Parametros By Gerson Villa Gonzalez Issuu
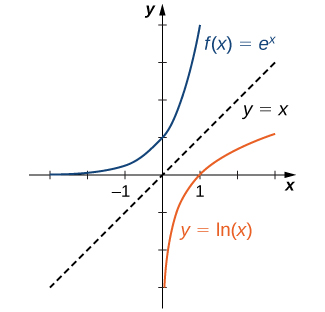



1 9 Limit Of Exponential Functions And Logarithmic Functions Mathematics Libretexts
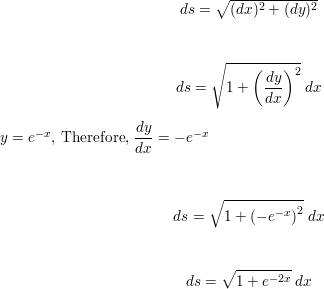



If The Infinite Curve Y E X X 0 Is Rotated About The X Axis Find The Area Of The Resulting Surface Homework Help And Answers Slader




Solution Of The Differential Equation 1 E X Y Dx E X Y 1 X



Find The Exact Coordinates Of The Centroid Where Y E X Y 0 X 0 X 3 Mathskey Com



Www Stat Auckland Ac Nz Fewster 325 Notes Ch3annotated Pdf




How To Show That E E X Mid Y Mid Y E X Mid Y Mathematics Stack Exchange



Ocw Mit Edu Resources Res 6 012 Introduction To Probability Spring 18 Part I The Fundamentals Mitres 6 012s18 L07 Pdf




If Xy Xe Y Ye X X 2 Find Dy Dx Maths Continuity And Differentiability Meritnation Com



Www Math Uh Edu Jiwenhe Math1432 Lectures Lecture04 Handout Pdf




A Sketch The Graph Of Y Ex As A Curve In R2 B Sketch The Graph Of Y Ex As A Surface In R3 C Describe And Sketch The Surface Z Ey Study Com
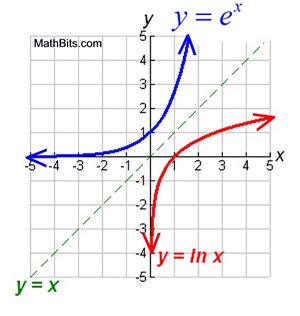



Natural Exponential Function And Natural Logarithmic Function Mathbitsnotebook Ccss Math




Ex 9 4 23 General Solution Of Dy Dx E X Y Is A E X E Y C




The Curve Of Exponential Function Y A X A X E X If A E And X 0 Download Scientific Diagram
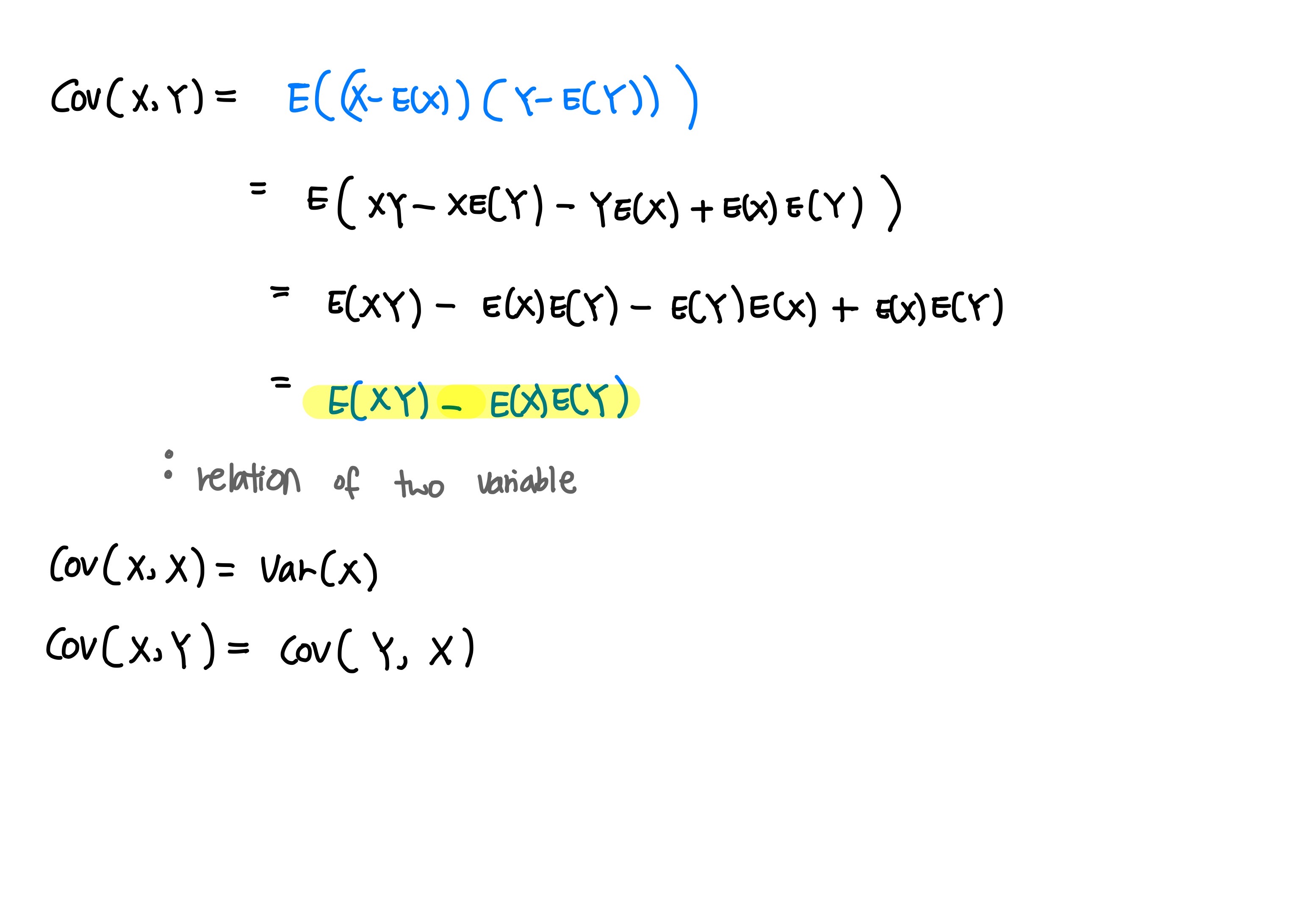



Covariance Correlation Coefficient Property Of Covariance




Natural Logarithms



Arc Length
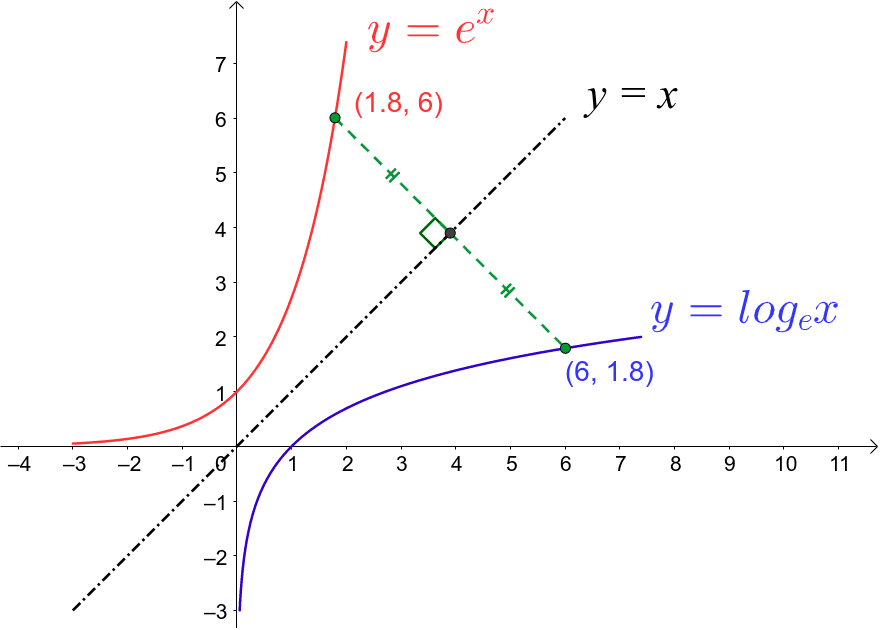



Graphs E X And Ln X Geogebra




Flat Function Wikipedia



How To Find X And Y Intercepts Of Graphs




The Derivative Of E X And Lnx




Misc 18 General Solution Ex Dy Y Ex 2x Dx 0 Miscellaneous



Ocw Mit Edu Resources Res 6 012 Introduction To Probability Spring 18 Part I The Fundamentals Mitres 6 012s18 L07 Pdf
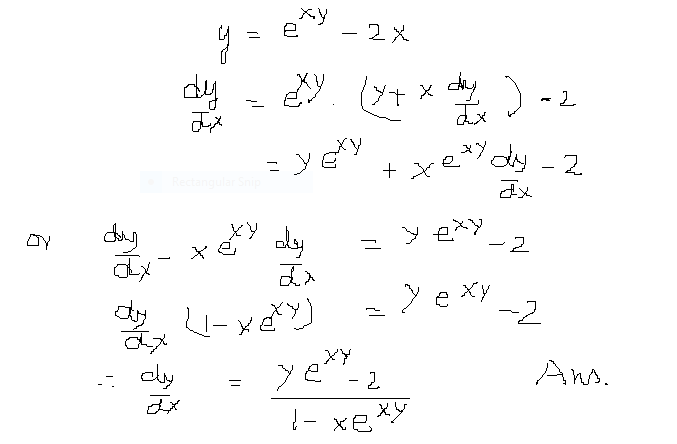



How Do You Differentiate Y E Xy 2x Socratic




Proof The Derivative Of 𝑒ˣ Is 𝑒ˣ Video Khan Academy
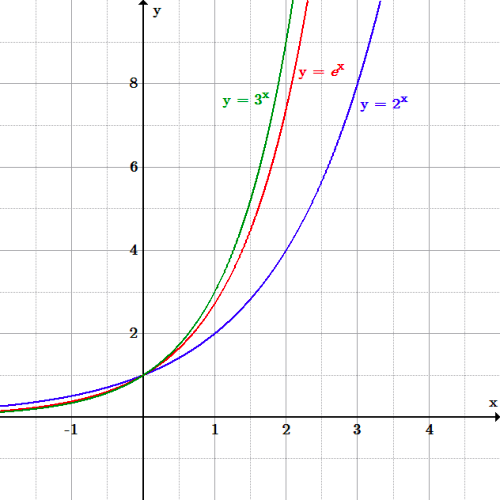



The Real Number E Boundless Algebra



0 件のコメント:
コメントを投稿